(1)ヴァイオリンが本来持っている音程の基本構造1(純正音程)
ヴァイオリンが持っている音程構造のうち、音の性質からただちに結論付けられるものが、弦長による音程の違いである(当たり前のことだが)。音程構造、などとご大層に語られるべきものでもないが、フラジオレット(ハーモニクス)の理解のためにも、波動の比を復習するためにも、弦長と音程の関係を見ておこう。
開放弦のG線上で、弦長と音の関係を確認する。音程は、弦長と反比例の関係にある。開放弦のG音を周波数1とすると、二倍音であるオクターヴ上のG音の周波数は2となる。弦の長さが二分の一になるとこの音を得ることができる。駒から弦長の二分の一のところが、ちょうどオクターヴ上のG音になる。この音は、きちんと押さえなくてもフラジオレットで取ることができることはご存知だろう。
次に、三倍音を考えてみよう。周波数比は1:3だから、弦長は三分の一になればよい。弦から三分の一のところを押さえると、開放弦からオクターヴと完全五度上のD音がでることがわかる。この音もフラジオレットで出るはずである。さらにその上の四倍音、五倍音(H)までは、フラジオレットで使用に耐える音である。
(問)G線上で、五倍音までのビットマップを作ってみよう
次に、弦長の比で各音をG線上で確認しよう。開放弦のG音から完全五度になるD音は、完全五度=2:3であるから、開放弦との弦長が3:2になるところに存在する。
開放弦から完全四度になる音(C音)は、開放弦との弦長が4:3のところにある。さらに、開放弦から長三度になるH音(G音との比は4:5)は、開放弦との弦長が5:4になるところに存在する。同様に、短三度になるB音は弦長が6:5、長二度(大全音A)は9:8、長二度(小全音A)は10:9、短二度は16:15(As)のところにある。
(問)開放弦G音から完全五度になるD音の図と同じように、上記のH、B、A(大全音)、A(小全音)、Asの各音を図示せよ。
この項の最後に、フラジオレットを考えてみよう。倍音列に当たるフラジオレットは、この項の最初に書いたように、2,3,4、5倍音のものが使用に耐えるものであるが、それ以外のフラジオレットはどうなっているだろうか。
まずは、開放弦から完全四度のところを軽く触って弾いてみる。すると、開放弦の2オクターヴ上の音が出るはずだ。
(2)ヴァイオリンが本来持っている音程の基本構造2(ピタゴラス音程)
ヴァイオリンなどの五度調弦の楽器は、本来ピタゴラス音律を再現するのに適している。理由は、五度調弦にある。感の良い人ならすぐわかるだろうが、ピタゴラス音律の基本は純正な五度を積み上げていったものであり、弦楽器の調弦そのものだからである。
ヴァイオリンの音程を語る場合、まず問題になるのが調弦である。五度を純正に調弦した場合、各弦の周波数比は、( ):( ):( ):( )になる。隣り合う弦同士は2:3になるので協和するが、一弦間に置いてしまうと協和しない。つまり、次のような音を重音で弾いたときに、和音として気持ちよいものにすることはできない。
(参考譜:下から順に、G、E、C、Eの重音)
〈 参考譜挿入予定 〉
これは、アンサンブルになるとさらに影響が大きくなる。純正に調弦された弦楽四重奏は、開放弦のC、GとEを同時に鳴らして純正な和音を作ることができない(ヴィオラのCまで拡大した開放弦の周波数比は、( ):( ):( ):( ):( )となる。このとき、C線とE線の比は( ):( )で、かなり絶望的な数値である(この問題を解決するために、弦楽四重奏の調弦はミーントーンで行うのが合理的であるが、今回はこの点については詳しく触れない)。
このように、ヴァイオリンを純正五度で調弦すると、和音を弾くときに不合理が生じる。しかし旋律を弾く場合、楽器本来の音程が非常に役に立つ。
G-Durのスケールを考えてみよう。純正の五度に調弦することで、各弦はG線から702セントずつ高くなっていく(平均律では5度は700セント)。すでに述べたように、五度は純正律もピタゴラス音律も同じであるので、スケールのD音は開放弦でよい。同様に、A、Eの開放弦も、開放弦のGを主音にとったときのG-Durのスケール上にある音である。このことは、開放弦と同じ音(オクターヴ違い)は全て開放弦と協和する音程で取ることができることを意味する。
*********参考(ストリング誌の連載から抜粋)***********
前項で述べたように、D線の1の指で押さえるE音は、正しく取ると開放弦と共鳴する音でした。同様のことは、G線上のA音でも起こります。また、ファーストポジションの3の指で押さえるG(D線)、D(A線)、A(E線)の各音は、一つ下の開放弦と共鳴するのでした。こういった音を正確に取ることが、再現性のある音程を得る最初のテーマです。
ヴァイオリンは「ピタゴラスの楽器」だと言われています。それは、各弦を完全五度に調弦するからです。このことをよく理解して耳を十分に使って音程を取ると、美しい音程感覚を身につけることができるようになります。最初に必要な感覚は、前回述べた純正な四度を聞きわけることと開放弦と共鳴する音程を正確に理解することです。
G線の開放弦からト長調のスケールを弾いてみましょう。調弦は純正に合わせてください(注)。第2音(A)は、D線とはもる音に取ります(これが四度の関係)。第3音(H)はE線のさらに上に開放弦があると仮定したH音の二オクターブ下になります。A線上の1の指で押さえたE線の開放弦とはもる(これも四度の関係)H音でもあります。第4音(C)は、G線の完全五度下のC音です。この音には直接確認する他の弦がありませんが、D線上に開放弦とはもるG音を取り、そのGとはもるCをG線上(五度)かA線上(四度)で求めることができます。第5音は開放弦のD音。第6音はA線とはもるE音。第7音(導音)も直接確認することはできませんが、理屈を言えば、先程の「仮想H線」のさらに五度上の「仮想Fis線」の音になります。この音は最後のG音に非常に近い音ですので、ほとんどの場合G音に対して指をぎりぎりまで近づけることでほぼ近い音が得られます。
**************************
以前、ある掲示板で、調弦を純正にするか平均律にするか、という論争を目にしたことがある。平均律であわせるべき、と主張した自称ヴァイオリン教師はともかく、その主張の尻馬に乗った「ヴァイオリン教師」が、「純正に合わせたら、調を変えるたびに調弦をしなければならない。そんなことはプロはしない」と書いていた。その知識のなさはお寒い限りだが、純正な五度調弦は、基本的に全ての調に対応できることを理解していただきたい。ただし、ある種の和音やアンサンブルになると事情が異なることは、すでに述べたとおりである。
長音階のスケールは、簡単のためにセント値を使うと

まず、G-Durで調べてみる。五度を純正に調弦した楽器のG線の値を、わかりやすくするために0セントとする。この時の開放弦は、D(702セント)、A(1404セント)、E(2106セント)になる。A、Eをオクターヴ下げる(1200セント引く)と、A(204セント)、E(906セント)となる。開放弦のGを主音とすると、D(第五音)もA(第二音)もE(第六音)もスケールの音律に乗っていることがわかるだろう。となる。このセント値で表された間隔は、調が何であっても変わらない。ヴァイオリンの上で開放弦が使えることを順に確認してみよう。
次にD-Durを見てみよう。開放弦のD音を0とすると各弦は、G(-702セント)、A(702セント)、E(1404セント)の位置にある。やはりオクターヴを変化させると、E(第二音・・204セント)、G(第四音・・498セント)、A(第五音・・702セント)となり、やはりピタゴラス音律に乗っていることがわかるだろう。
(問)同様に、A-Dur、E-Dur、Fis-Durを調べてみよ。
シャープがひとつずつ増えると、調性は五度ずつ上がっていくことはおわかりだと思うが、シャープがつく音も開放弦の順に上がっていく(F→C→G→D→A→E→H→)。これがまさにピタゴラス音律の作り方と同じであることに気づくと、ヴァイオリンが「ピタゴラスの楽器」だという意味が理解できるだろう。
更に、開放弦を下がっていく方向に確認してみよう。C-Durの主音は、開放弦のGから702セント下のC音(ヴィオラの開放弦のC)のオクターヴ上を主音に取る。この音は、参考資料のとおり、G線の開放弦から順にピタゴラスの全音と半音で取ったCと等しくなる。開放弦のGからの距離は、204+204+90=498セント。G線の開放弦から702セント下に取ったC音をオクターヴ上げると、-702+1200=498となって、一致する。この音を主音にとって、各開放弦を確認してみると、シャープ系と同様に、開放弦を全て使えることがわかるはずである。更にフラットを増やしていくと、F-Durの場合は、E線の開放弦から90セントのF音を主音に、B-Durは開放弦のA線から90セントのB音を主音に取ればよいことが確認できるはずである。
(問)C-Dur、F-Dur、B-Dur、Es-Dur、As-Durの各調で、開放弦が使えることを同様に確認せよ。
ピタゴラス音律を理解していれば当然のことであるが、このように完全五度を純正に調弦した弦楽器は、ピタゴラス音律の上にある音を主音に取れば、全ての調で開放弦を利用したスケールを得ることができる。これが、弦楽器の音程の基本構造である。
(3)シャープとフラットの話
ピタゴラス音律の解説だけで本来は全てを語っているのだが、確認のために、シャープ、フラットの考え方を簡単にまとめておく。
本来、シャープ、フラットは「元の音よりやや高く、またはやや低く」という意味であった。この意味では、例えばGisはGより少しだけ高い音であって、Aより少しだけ低いAsよりも低くなる。和声的に言えばこれが自然になるが、ヴァイオリン(旋律楽器、ないし旋律的音程)では、この高低関係は逆転する(詳細は、音律の歴史を学ぶ必要がある)。
ピタゴラス音階の全音である204セントを半音で分割するときには、真中(102セントの位置)ではなく、90セントと114セント(ないしは114セントと90セント)に分けることになる。どちらになるかは、音階のセント値を考えれば理解できるだろう。
Es-Durを例にとってみよう。音階は以下の通りになる(数字は、主音を0にしたときの各音の主音からのセント値)が、これに、基音(ピアノの白鍵)を書き加えてみる。
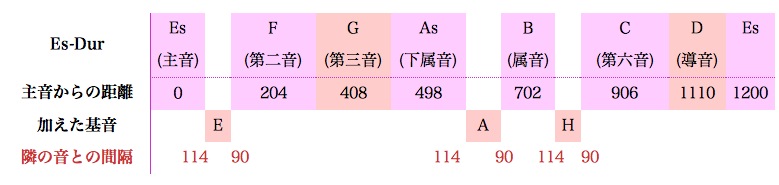
ごらんの通り、フラットのついた音は、元の音から114セント下、すなわち元の音のひとつ下の音から90セントの位置にある。同様に、Fis-Durを考えてみる。

この「24セント」は、あなどりがたい量である。114セントの半音と比べると約24%、90セントの半音からは実に約26,7%もの違いがある。このことをよく理解して、シャープやフラットの音程に注意を払ってほしい。ここまでくれば、「異名異音」(異名同音ではない!)が理解できるはずである。AisはAから114セント、Hへ90セントの位置にあり、B(Aから90セント、Hへ114セント)とは24セントの違いがある。同様に、Fis-Durの導音であるEisは、Fisから90セント下の位置にあり、F(Fisと114セント離れている)とは違うところにあるのがわかるはずである。
(4)基本の「音程ビット・マップ」
ヴァイオリンの音程基本ビット・マップは、よく言われている「四つの基本形」に対応したものである。
ヴァイオリンの音程は、基本的に以下の四通りの指の形でできている。
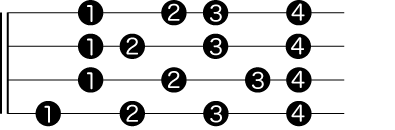
1)2,3指が半音になるもの
2)1,2指が半音になるもの
3)3,4指が半音になるもの
4)開放弦と1指が半音になるもの
それぞれについて、音程を確認してビット・マップを作ってみよう。もちろん、ここで言うところの「半音」とは、ピタゴラス音律の半音(90セント)である。
1)2,3指が半音になるもの
G線上では、2,3指が半音になる時の音程は、開放弦から順に、G、A、H、C、Dとなる。これは、Gを主音に取ったときの長音階のドからソまでにあたる。他の開放弦も同様である。このパターンをビット・マップにしてみよう。
2)1,2指が半音になるもの
この場合は、G線上で、G、A、B、C、D、となり、Gを主音に取った時の短音階になる。1)と同じようにビット・マップを作ってみよう。
3)3,4指が半音になるもの
同様に考えると、G、A、H、Cis、Dとなる。音階に当てはめると、Dが主音の長音階での「ファ」から「ド」までとなる。同様に、ビット・マップを作ってみよう。
4)1,2指が半音になるもの
同様に、G、As、B、C、Dとなる。これはEs-Durの「ミ」から「シ」までとなる。同様に、ビット・マップを作ってみよう。
いずれの場合も、もちろん各音程の間隔は、全音=204セント、半音=90セントになっている。この四つのパターンを組み合わせると、(開放弦を含む)全ての調性のスケールを得ることができる。
(問)理解を確認するために、シャープ四つまでとフラット四つまでの各長音階の音程マップを作ってみよう。
(5)和音用ビット・マップ
通常の旋律音程を演奏するときの指の位置は、前項で述べたビット・マップに従えばよいことが理解されただろうか。次に、和音を奏する時の音程について考えてみよう。この場合も、調弦が純正な完全五度になっていることを前提とする。
1)開放弦と協和する音たち・・その1(開放弦にある音)
まず、開放弦と協和する音程がどの位置にあるかを確認する。
*** 参考資料:同じEでもおさえる場所が違う?(大三元さんのサイトからの引用)***
ヴァイオリンD線、第一ポジション、第1指で弾くEに就いて考えてみる。次の譜例を参照する。

1. 先ずヴァイオリンの調弦は第一小節のようにするが、ここでD音はG音より丁度1.5倍周波数が高い。或いは、Gの周波数:Dの周波数 = 2:3 という単純な整数比になっている。これが最初の重要なポイントだ。二つの音の周波数比が単純な整数の比率で表される場合に「音が合ってる、ハモってる」ということになる。そういえば、オクターブってのが周波数比が 1:2 のことを言うことは知ってる人も多いだろう。
2.そして(いちいち「周波数」と書くのはやめるが)D:A も2:3 なのだ。同様にA:E も 2:3だ。これを全部G=1として表現するならD=3/2、A=(3/2)*(3/2),E=(3/2)*(3/2)*(3/2)、となる。表にまとめておくと
E (3/2)^3 27/8 660.00
A (3/2)^2 9/4 440.00
D (3/2)^1 3/2 293.33
G (3/2)^0 1 195.56
音 周波数比 左を計算すると A=440Hzとすると
3. さて、譜例の第3小節目から考える。全音符で示したE+Aがよくハモるようにするにはどうするか。全音符で示したEのオクターブ上に開放弦のEがある。これが開放弦Aを440Hzとした時に、開放弦Eは660Hzになっている。そのオクターブ下とは、2で割れば良いから、330Hzということになる。これ(330Hz)と開放弦A(440Hz)とは3:4という単純な整数比であり、良くハモる。
4. 次に譜例の第2小節目のG+Eをハモらせるにはどうするか。仮に上記3.の場合と同じ場所を押さえて330Hzを出すとしよう。開放弦のG195.56HzとはAの(2/3)に相当するDの更に(2/3)のことだ。つまりAの4/9に相当している。これとAの3/4に相当するEの関係はどうなるか。(4/9):(3/4)ということは 16:27 ということである。さて、これは単純な整数比だろうか???
5.自然倍音という倍音列がある。例えばホルンの原理(?)としてガスのホースにマウスピースをつけて吹いてみると一番低く共鳴する音がある。これを仮にド1とする。も少し強く吹くと、そのオクターブ上のド2が出る。これを2倍音という。更に上の方を探って行くとド2の完全5度上であるソ2が出る。これを3倍音という。その次に出てくるのが4倍音、さて、何の音だろうか。そりゃそうだ、4倍音とは2倍音のオクターブ上だ。つまりド3とでも名づけようか。その次にミ3とでも呼ぼう第5倍音が出てくる。
6.これが今求めようとしているGに対する、ハモるEを決めるのに重要なことだ。つまりド3とミ3の関係が4倍音:5倍音ということだ。少し戻って、ソ2とミ3の関係は、3:5ではないか! これがGに対して求めていた良くハモる方のEだ。
7.先に周波数を計算してしまうと、Gの195.56Hzの(5/3)倍がハモるEだ。 325.9259Hzと計算された。
8.大変だぁ。さっきAと合わせようと思った時のEは330Hzだったのに、今度Gと合わせようとすると、約326Hzにしなきゃならん。。。ここの約4Hzの差、ってのは1%以上の違いだ。(正確には1.25%の筈)ヴァイオリンの弦の長さを約30cmとすると、その1%は3mmだ。その位の微調整をしないと合わせるべき音に対する sweet spot が違うんだ。
9.こういうことを各調に対してリアルタイムに実行して行くと「良くハモる音程だ」と言われるようになる、、、のだろう。。。 ところが一方メロディラインの場合には330Hzの方のEを弾くのが「気持ちが良い」とされる。奏者は従って、各場合がメロディラインを大事にするか、ハモリをより大事にするか、を決めて、それに沿った「周波数」を「出力」することが、どうやら、求められるらしい。
10.ここにE音を例に挙げたがこの音はハ長調ならミだが、イ長調ならソに相当する音だ。上に数字を挙げて説明したのは、他でもない、同じE音でも、ハ長調のミに相当する時とイ調のソとして使われている時では出すべき音の高さ(周波数)が違う、ということだ。
11.さっき、ゴムホースの話を書いたが、実はヴァイオリンでも倍音(複数)を出すことが出来る。G線の高い方で、指を滑らせながらフラジオレットを出すと色んな自然倍音の音が出てくる。開放弦のGをG0と呼ぶと弦長の丁度半分がG1、そのまた半分の場所でG2が出る。G1が出る場所とG2が出る場所の中間にD2が出る場所があるだろう。弦を3等分した位置の筈だ。G2(4等分の場所)から更に上の方へフラジオを探して行くと、ソシレソ(G2,H2,D3,G3)って出て来ませんか? このG2とH2が長三度。意外に狭い(H2って低い)と思いませんか? これが和音を造る時の正しい長三度なんだそうです。
12.良くハモる三度(純正三度)と、メロディラインで使う三度(ピタゴラスの三度)などを視覚的に表現したのがリサージュ図形です。御覧あれ。
****************************
上の参考資料にある「開放弦にハモるE」を実際に探してみよう。
基本のビット・マップにあるE音は、開放弦のD音から204セントの位置にある。資料にあるように、この音はE線の開放弦と1:2の関係になっていて、A線の開放弦と協和する関係になっている。これが開放弦Gと協和しないことはわかるだろうが、それでは、G線と協和するE音はどこにあるのだろうか。音律ごとの音程のセント値を見れば一目瞭然だが、理解を深めるために少々面倒な方法を採用してみよう。
開放弦のG音とD線のE音は長六度の関係にある。これは、短三度が逆転したものであるから、G音と協和するE音を比で考えると、
E音:G音=5:6より、G(-1)音:E音=3:5
となる。開放弦のD音は、開放弦のG音と比べると、2:3の関係になっているので、
G(-1)音:D音:E音=6:9:10
となり、D音:E音の関係は9:10になるのが正しい。同様に、開放弦のA音と協和するE音を比で考えてみると、
E音:A音=( ):( )(完全四度の関係だから)
D音:A音=2:3
ゆえに、D音:E音=8:9、となる。上記の9:10と比べてみると、
D音:E音(Gに協和する):E音(Aに協和する)=72:80:81
となり、G音に協和するE音と比べて参考資料のような差になる。この数値(80:81)を見て「おや」と思った人も多いだろう。あちこちで目にしているであろう「ピタゴラス・コンマ(シントニック・コンマ)」である。この全音の違い(8:9と9:10)が、大全音と小全音である。
(問)上記の二つのE音を、D線上でセント値を用いてビット・マップにせよ。同様に、A線上のH音、E線上のFis音をビット・マップにしてみよ。
2)開放弦と協和する音たち2・・・ドミソの「ミ」
A線とE線の開放弦は、A-Durの「ド」と「ソ」であるが、ここの「ミ」であるCis音を入れてみよう。協和する音程がどこにあるか考えてみる。
協和する長三和音の周波数比は4:5:6であるから、開放弦と協和するCis音は、この比率になるところに存在する。これに対して、基本のビット・マップにあるCis音がどこにあるかを考えるために、純正五度を積み重ねてみると、
A → E → H → Fis → Cis
( ):( ):( ):( ):( )
となるので、Cis音をA音と同じオクターヴの中に下げてA音との比を求めると、A:Cis=( ):( )となる。これを協和するCisと比べると、
A音:Cis音(A、Eと協和する):Cis音(ピタゴラスの音律に乗った音)=( ):( ):( )
となる。この差がかなりのものであることは一目瞭然だろう。
(問)各開放弦上の2の指(和声で・・音はH、Fis、Cis、Gis)のビット・マップを作ってみよう。
(6) 分散和音とクロマティック・スケール
分散和音とクロマティック・スケール(いわゆる半音階)についても述べておこう。分散和音は、英語(Broken Chord)で書かれている通り、和音を「壊した」ものである。スケール同様、基本練習として欠かせないものであるが、音程に注目してしっかり理解しておこう。
近代的なヴァイオリンのトレーニングで使われる分散和音は、以下の7通りである。
- 135(長三和音)
- 13^5(短三和音)
- 146(四六の和音)
- 146^(短三和音の第二展開形)
- 136(短三和音の第一展開形)
- 1357^(属七の和音)
- 13^5^6(減七の和音)
(注)私のカルテを見ている人にはおなじみだろうが、これらの数字は、調性の中で何番目の音かを指す。1は主音(ド)、5は属音(ソ)という具合である。ちなみに、「3^」の「^」は、半音下を指す。
基本的には、これらの音程は、ピタゴラス音律に乗った音で取るべきであるが、少ない音を繰り返して使う場合などで和音のように聞こえる効果を意図して書かれている場合は、純正な音程で取るべき場合もある。
(補足)分散和音の連続を純正に取るべき代表的な例は、モーツァルトによく登場する「ドミソミドミソミド」などの形だろう(譜例参照)。モーツァルトは、当時評価され始めていた機能和声向きの音律(ヴェルクマイスターなど)に対して、長三和音が美しいミーントーンを用いていた。そのために、長三和音や三度が繰り返される形を好んで使ったという。ピアノを習った人なら、モーツァルトや同時代の作曲家がこの形を多用したことに気づいていたはずである。だから、平均律に調律したピアノでこの形の音形を無神経に弾くことは、モーツァルトを理解していないことと同じである。
半音階は、平均律的に取ると、どこから始まってどこへ向かうのかがわからなくなる。それを避けるために、二つの半音(90セントと114セント)を正確に使い分けることが必要である。
半音階は、オクターヴが12音であることを利用して、4つずつに分けて練習する方法がある。音の並び方は(ただし、⇒は114セント、→は90セント)、
C⇒C♯→D⇒D♯、→E→F⇒F♯→G、⇒G♯→A→B⇒H→C
と考えるわけである。C→E→G♯の流れを、長3度の連続と覚えればよい。
(注:この点について、「弦楽器のイントネーション」P.61の記述には問題を感じる。CEGisを「増三和音であって、共鳴音がEに収束する」と書かれているが、Cを固定してEを旋律的に取るなら共鳴音は収束せず、Eを和声に取るとGisが低くなりすぎる。Eを開放弦に固定するとCが矛盾をきたす。仮に、Gisを低く取らせるのであれば、Asと記すべきであろう。無理に和声として考えることはないと考える)
(注:半音階の記述法は混乱している。カール・フレッシュのスケールなどのスケール・テキストでも、シャープとフラットを混用しているケースが少なくない。基本的な練習は、上記の記法に従って欲しい)
半音階をこのように取ると、平均律に塗りこめてしまったものとは比べようもないほど活き活きとしたスケールになる。始点もはっきりして、和声の中で違和感のない音階になる。この音程感覚を十分に身につけていただきたい。
(7) テンポや音の形と音程の関係
最後に、テンポと音程の関係について簡単に述べておこう。
縦の音程(同時に鳴る二音以上)は純正に、横の音程(旋律進行の音程)はピタゴラス音律に則って、ということが原則であるが、この原則はさまざまな要因で例外を生む。前章の「音律を学ぶことの意味」でも述べた、時代や楽曲による差異がまず一つ。アンサンブルや楽器による音程の違いがもう一つ。そして、ピタゴラス音律が持っている性格そのものからくる、テンポの差異による音程の違いである。
人間の耳が、同時に鳴る純正な二音や、ピタゴラス音律に則った旋律音程を心地よいと感じることはすでに述べた。では、進行さえすれば、常にピタゴラス音律が気持ちよいのだろうか。
この点については、講習会で実験して納得していただくが、非常にゆっくりと旋律を弾くと、ピタゴラス音律の心地よさは失われる。特に重音進行では、そもそも純正な和音が前提としてあるために、横の結合は弱くなり、ピタゴラス進行が求められないことも多い。純正な音程を取るか、ピタゴラス進行を選択するかは、縦の結合が強いか、横の結合が強いかという選択の問題に帰着する。この時に、テンポが重要な要素になる。テンポが遅くなると横の結合は弱くなる。
また、ピタゴラス音程も常に同じでよいわけではない。テンポが速くなればなるほど、半音と全音の差が強調されなくてはならない。しかし実際は、テンポが速くなると指が平均化しようとして、半音と全音の差が小さくなっていく。この点が難しいところである。講習では、その違いを理解していただく。



