(1)音律とは何か
結論から言うと、音律とはオクターヴをどのような間隔に分割するかという方法を示す。音律、すなわちオクターヴの分割方法はさまざまに提唱されてきた歴史的経緯がある。ヴァイオリンの演奏のために理解する必要な音律は、純正律、ピタゴラス音律および平均律の三つである(室内楽の場合ミーントーンを理解していた方がよいこともある)。各音律の違いは次項以下で述べるが、簡単に音律が必要である理由と歴史的な経緯を述べてみよう。
オクターヴが美しい音程であることは、古代ギリシャの時代よりはるか前から知られていた。単純な振動を図ることはそれほど難しいことではなく、1:2の振動比がオクターヴを作ることや、2:3の振動が美しいものであることも良く知られていたのである。この2:3の音程を積み上げ、さらにオクターヴ内に配列すること(ペンタトニック・・ピタゴラス音律の項参照)で、耳に心地よい音のつながりができることは、それまでも用いられていた旋律を作る手法だったが、ピタゴラスはこのことを論理的に証明した。ところが、2:3の比率で作った音を繰り返して積み上げてオクターヴ内に配列すると、最終的に矛盾ができることははじめからわかっていた。その矛盾は、矛盾としていわば「諦められて」いたのである。
(補足)実際にどのような矛盾が生じるかということは、すでにあちこちに書いているので復習して欲しい(拙著「今から初めて上手くなる、楽器とオーケストラ」42ページ以下など)。前章で述べたような知識を前提とすれば、これまでわからなかった人も理解できると思う。
単純な旋律が主流であった時代は、このピタゴラス音律が主流であった。このことは、ギリシャから広がった欧州だけでなく、日本でも、旋律をピタゴラス音律に沿ったものとしていたことからもわかるだろう。
(補足)日本でもピタゴラス音律を使っていたという一つの証拠が、邦楽の旋律が「四七抜き(ペンタトニックのこと)」でできていることである。「四七抜き」とは、音階の第四音、第七音を用いない、1,2,3,5,6,8というつながりが、旋律用のオクターヴの分割となっていることを示す。そのしきたりに沿ったものは、現在でも童謡などで見ることができる。例えば、「赤とんぼ」の音階配列は「ソドドーレミソドラソ、ラドドーレーミー、ミラソーラドラソラソミ、ソミドミレドド」となり、「ファ、シ」が用いられていないのがわかるだろう。この「四七抜き」の音律が使われていたのは、日本だけではない。
中世になると、教会音楽が全盛となり、多声音楽(ポリフォニー。これに対して、主声部が一つである音楽をモノフォニーと呼ぶ)が発達した。声部が複雑になるにつれて、同時に鳴る音の心地よさが追求されるようになると、次項で述べるような自然倍音によって構成された純正律が重視されるようになった。もちろん、純正律も万能ではなく、単に同時になった時に一番気持ちの良い音程だ、というだけである。特に、純正律は調によって全く音程が異なるために、音程が固定されている楽器には全くそぐわないものであった。
実際の音程としては、純正律とピタゴラス音律がもっとも乖離したものが多い。加えて「和声には純正律、旋律にはピタゴラス」という単純な図式が成立することはなく(特に、残響が長い中世の演奏会場では、旋律をピタゴラス音律に則って演奏することが問題となることもある)、実際の演奏にどのような音律を使ったらよいのか、ということは、解決しない問題として残ってしまった。この問題を解決するために、さまざまな工夫がなされていく。また、音楽が和声の働きが重要な役割を持つようになり、さまざまな転調を要求するようになると(機能和声)、純正律やピタゴラス音律などではない音律が求められるようになってきた。
モーツァルトの時代まで、ミーントーンと呼ばれる音律がよく使われていた。ミーントーンは、後で述べるように、三度が美しくなるように考えられた音律だが、やはり調性に制限が大きい。そうした中で、より転調が容易で全ての調性にバランスが取れている音律が求められるようになり、登場したのが、ヴェルクマイスターやキルンベルガーなどの調律法である。これらの音律は、できるだけ純正に近い響きを残しながら、転調しても音の不整合が少なくなるように考えられているが、もちろん万能ではなかった。
(補足)この話もどこかに書いたが、バッハの「平均律クラヴィーアのための・・・」と邦訳されている曲集の「平均律」は誤りである。バッハの時代には現代使われている平均律は用いられていない。バッハが愛用した音律は、ヴェルクマイスターの第三調律法と呼ばれるものであり、この曲集も当然ヴェルクマイスターで演奏された。ヴェルクマイスターは、純正律やピタゴラスは言うまでもなく、ミーントーンと比べても、各調の差が少なく転調機能に優れているが、それでも平均律とは似ても似つかぬものである。実際にチェンバロを調律して比べてみると、誰でも違いがわかるだろう。
平均律が歴史に登場したのは16世紀後半と言われているが、純正な響きを(オクターヴを除いて)一つも持たないこの音律は、美しくないものとして大きな潮流にはならなかった。19世紀に入り、現代のピアノに近い楽器が普及を始めると、さまざまな理由から平均律が広がっていく。こうして、19世紀後半以降の作曲家は、平均律を前提として曲を作るようになっていった。
(2) 音律を学ぶことの意味
日本では、音程の教育がほとんど放棄されている。ヴァイオリンに限ったことではないことはサイトにも書いたが(音程の良いピアノ、悪いピアノの話など)、音程の重要性は、ただ単に「気持ちよい音で弾く」ことにとどまらない。曲をどのように弾くか、という問題にも深くかかわっている。今回の講座は入門編で、ヴァイオリンが表現できる音程を理解することに主眼があるが、音律を学ぶことの意味を、少しだけ深く理解していただきたい。
有名な話だが、モーツァルトの曲には短調のモノが非常に少ない。中学生の頃「モーツァルトは人を楽しませるために音楽を書いたから短調が少なく、ベートーヴェンは苦しみを表現するために短調の曲をたくさん書いた」という某音楽評論家の記述を読んだことがあるが(愚かにも、当時の私はそれを信じてしまったのだが・・)、これが一面的で的外れであることは、音律の歴史からも説明ができる。
モーツァルトは、若い頃(ヴァイオリニストとして活躍していた10代のころ)には、チェンバロを用いていた。その後、性能の良いピアノフォルテを手に入れた。これらの楽器たちは、当時の流行に従ってミーントーンに調律されたものだった。ミーントーンは、C-Durが最も美しく、調性記号が増えるに従って矛盾が大きくなる。それと同時に、短調は非常に難しい。従って、短調の曲は数が少ないだけでなく、種類も少ない。交響曲もカルテットも2曲ずつしかない。こうした事実を理解していると、アンサンブルなどでどのような音程をとるのか、ということのヒントになることは多い。
ベートーヴェンになると、音律の影響は更に重要性を増す。ベートーヴェンは、初期の頃ミーントーンに調律した楽器を使っていたと言われているが、すぐにキルンベルガーに移行する。キルンベルガーはバッハの弟子で、ベートーヴェンに大きな影響を与えた。キルンベルガーは調性を3分類し、それぞれの性格を明確にした。ベートーヴェンの楽曲は、ある時期以降、この調性の性格を十分に反映して作られている。
(注:キルンベルガーの3分類は、古典派からロマン派初期の音楽を理解するために重要なカギになる。今回は詳しく触れないが、「楽曲解釈法」の講座で取り上げることになるだろう。簡単な記述は、ストリング誌の川島先生の連載にある)
モーツァルトとベートーヴェンを俎上に乗せたが、他の作曲家でも音律・音程の問題が作曲家の意図を知るために重要な要素となることは多い。
3) 純正律
ある物体が振動するとき、その振動数の自然数倍の波を同時に発している。例えば、100Hzで振動する物体は、200、300、400、500・・・Hzの波も同時に起こしている。音について考えてみると、この音のうち、始めのいくつかはお互いに単純な整数比になっている。これらの音を取り出すと、協和する音程になる。
自然倍音列:1(基音)、2(2倍音)、3(3倍音)、4(4倍音)・・・
第一章での説明を思い出してみよう。100Hzで音を出したとすると、200Hzの音は最初の音のオクターヴ上(1:2だから)になっている。次の音(300Hz)は、二つ目の音(200Hz)と比べると2:3になっているので、二つ目の音の完全五度上であることがわかる。100Hzというのはあくまで計算しやすいように取った値であり、実際は具体的な音(実際の周波数)とは無関係に自然倍音列が存在している。
いろいろと話をしていると、この点がよく理解できていない人が多いようである。上の例では、基音を100Hzとしたが、基音が120Hzであれば、2倍音は240Hz、3倍音は360Hz・・・にな、これらが同じように基音、オクターヴ上、その五度上・・・と連なっていることがわかっただろうか?
このように取り出した自然倍音列をオクターヴの上に並べなおしたものを基本にして作られたものが純正律の音階である。純正律は、同時に鳴ると耳に心地よい音程で作られているので、和音を作るのに適している。
ここで、基音を100Hzとしたときの純正律の音階を考えてみよう。自然倍音列がどのような音になっているかを検証してみると、
- 100(基音、仮に「ド」としておく)
- 200(基音のオクターヴ上の「ド」)
- 300(2倍音の上の「ソ」、これを基音と2倍音の中のオクターヴの中に入れるためには、オクターヴ下げればよい。下げた周波数は( )となる)
- 400(基音の2オクターヴ上の「ド」)
- 500(400の「ド」のすぐ上の「ミ」、これを最初のオクターヴに入れるためには、2オクターヴ下げる必要がある。下げた周波数は( )となる)
- 600(300のオクターヴ上の「ソ」)
- 700(その上の「シ」のフラットより低い音)
- 800(3オクターヴ上の「ド」)
- 900(その上の「レ」)
- 1000(その上の「ミ」500のオクターヴ上でもある)
- 1100(その上の「ファ」のシャープより低い音)
- 1200(600の「ソ」のオクターヴ上)
- 1300(その上の「ラ」のフラットよりかなり低い音)
- 1400(700のオクターヴ上)
- 1500(その上の「シ」)
- 1600(4オクターヴ上の「ド」)
となっている。この数値は、セント値ではなく周波数であることを忘れないで欲しい。
ここで登場した音たちを、オクターヴの中に格納してみよう。例えば、300Hzの「ソ」は、二で割る(オクターヴ下げる)と150Hzとなり、100Hzから200Hzの中、すなわち最初のオクターヴに収まる。これを同様に繰り返すと(ここに登場しない音は天下り的に示す)、
- ド:100Hz・・「ド」に対して1:1
- レ:112.5Hz・・同様に、8:9
- ミ:125Hz・・・・・・・4:5
- ファ:133.33Hz・・・・3:4
- ソ:150Hz・・・・・・・2:3
- ラ:166.67Hz・・・・・3:5
- シ:187.5Hz・・・・8:15
となる。ここに登場しない音たちは、(やや天下り的だが)音律表で他の音律との差を確認していただきたい。
こうして作られた音律は、旋律を弾くことには全く適さない。というか、不可能であろう。また、主音を基準に単純な比で他の音が求められるために、主音を変えると他の音が全部違ってしまう。純正律にチューニングした鍵盤楽器が存在しないのは、それが大きな理由である。「C-Dur用の楽器」「D-Dur用の楽器」などを全て別々に用意しなくてはならなくなるのだ。音律の議論を嫌う人たちがよく用いる手法だが、調性によってチューニングを変えなければならない音律はそもそも無駄である、という論拠になっている(もちろん、この議論には全く意味がない)。
(4)ピタゴラス音律
ピタゴラス音律は、純正五度を積み上げた音程を基本とする音律である。
まず、ペンタトニックを説明する。言葉が難しいと感じるかもしれないが、これは前述のとおり、「四七抜き」と覚えればよい。
基本となるC音の純正五度上はG音、さらにその五度上はD音、A音、E音と続く。このD音~E音までをオクターヴ内に収めると、C、D、E、G、Aという五つの音列ができる。これを、ペンタトニックと呼ぶ。各音の周波数比は、C:G=2:3、G:D=2:3、D:A=2:3、A:E=2:3であるから、
C:D=( ):( )、C:E=( ):( )、C:G=( ):( )
C:A=( ):( )となる。
この配列で並んだ五音が心地よい旋律を作ることは、前述したように、世界各地で「四七抜き」の旋律が使われたことでも明らかだろう。さらに、D:E、G:Aを求めてみると、共に( ):( )になることがわかるはずである。すなわち、ここに登場した全音(CD、DE、GA)は、すべて( ):( )になっている。
これを利用して、残りの全音を推測してみよう。FはGから全音下がったところにあるので、F:Gも( ):( )にあるように取ってみる。この時、E:Fは( ):( )となる。さらに、Aの上のHを考えてみよう。A:Hがやはり( ):( )になるように取ると、H:C(+1)は、E:Fと同じ( ):( )になることがわかるだろう。この全音の比が、セント値で表した全音、204セントであり、半音の90セントである。
このように、ピタゴラス音律では、全音の幅も半音のそれも全て同じである。
この方法は、本来の音律の求め方ではないが、本来の求め方で確認してみよう。基準になるC音から、上下に完全五度ずつ積み上げていく。
C→G→D→A→E→H→ Fis→Cis→Gis→Dis→Ais→Eis→His→
←Fes←Ces←Ges←Des←As←Es← B← F← C
このように五度を積み上げていくと、12の音がすべて登場する。音律表で確認していただきたいが、この五度は平均律と比べて2セント広く、基準から遠くなればなるほど、平均律からは乖離する。上に積み上げていくと、右へ一つ移動するたびに2セントずつ差が広がり、下に降りていくと、左に進むたびに2セントずつ下に差が広がる。くどいようであるが、平均律との差を見やすくまとめてみる。
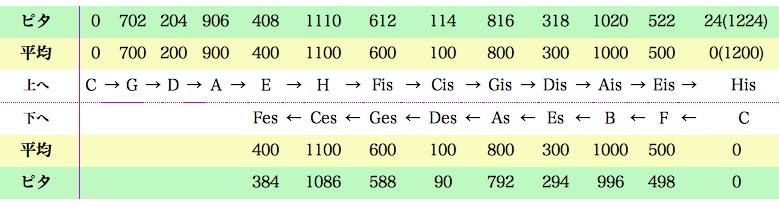
異名同音が、上下ですべてピタゴラスコンマ分(24セント)ずれていることがおわかりいただけるだろうか。これが、ピタゴラス音律を構成する音なのだ。
(5)平均律
平均律が登場した歴史は、以外に古い。16世紀にはガリレイが半音を17:18に取る平均律を見つけて、実際に利用されたようである。この比で与えられる半音は、現在の12音平均律よりごくわずか狭い(18/17を12乗すると、約1.98556となる)が、計算値としての平均律も、ガリレイがこの平均律を見つけた直後に考案されている。
平均律の最大の利点は、調性による差異がなく、転調が容易であることだ。また、楽器による差異を標準化しやすいという利点もあった。しかし、耳に心地よい音程がオクターヴ以外に存在しないという欠点は決定的で、平均律が普及するのは19世紀後半以降になる。
純正律とピタゴラス音律で音程を組み立てられる弦楽器だが、われわれは平均律についても理解が必要である。ピアノと合わせることはいつでも起こることであるし、オーケストラなどに参加したときには、やはり平均律と向き合う必要が生じる。前述のように、平均律を前提として作られた楽曲も少なくない。純正律とピタゴラスを前提とする音程楽器でどのように平均律に対応するか、という問題は、音程講座の上級編の話題であるが、ここでは基本的な問題点と知っているべき知識を提示しておく。
弦楽器を演奏するときに知っておくべき平均律のポイントは、音律上、音程の乖離がどうなっているかということである。理論値は、音律表を見ていただければわかるだろう。現実にピアノとあわせるときにどのような音程を取るか、というや、アンサンブルでどのように対処するか、という点については、音程講座の実戦編で詳しく解説する。



