（１）音程を考える順序

実際の音程理論に入る前に、ヴァイオリンの音程を論じるときに必要なことを、まず流れとして把握していただきたい。音程を考える考え方そのものを理解していない方があまりに多いからである。簡単にまとめると、ヴァイオリンの音程を考えるまでの道筋は以下のようになる。

１）音程を決めるのは、振動数である。音律の根本は、音の間隔を周波数比で表すことで理解できる。

２）どのような音を人間は心地よいと感じるか

→　心地よい音程は、同時に複数の音が鳴る時と、音が時間経過とともに動くときで違いがある（これが根本）。前者が和声（和音）であり、純正律が相応しい。後者が、メロディを構成することになり、ピタゴラス音律が相応しい。

３）ヴァイオリンの調弦を純正な完全五度に合わせた上で、これらの音律に則った音程を探していく。ただし、ヴァイオリンの上の音程を考える上で周波数比を用いることが困難な場合があり、音程の違いを理解するためにオクターヴを人工的に配分した「セント値」を用いる（平均律では、オクターヴを1200セント、つまり半音一つを100セントと呼ぶ）。

４）音程の原則を知って、正しい音を作り出すことができるところから作っていく。

何事を学ぶときでも、頭をどのように使うか、どんな順序で考えるかということを見失ってはならない。わからなくなったら、思考を巻き戻して考え直してみる努力を怠らないことが必要である。また、自分が何を理解できていないかを常に気にして欲しい。

（２）波の基礎知識

音は波である。よく「空気の振動」とされているが、正しくない。水中で音が聞こえることはみなさんも体験したことがあるだろう。人間が音を認知することは、鼓膜がある一定の振動を捉えて電気信号に変換し、それを脳が認識することである。音とは、本来は波を伝える非常に広い範囲の現象のことである。波の振動は、一秒あたり一回の振動を「１Hz・・ヘルツ」と数える。

人間が音として認知できる波の振動数は、20ヘルツ（１秒間に20回の振動数）から20000ヘルツほどの限られた範囲の縦波しかない。20ヘルツ以下の音を「超低周波音」と呼び、モーターや工事現場などで発するものが環境問題として取り上げられることも多い。一方で、20000ヘルツ以上の振動を「超音波」と呼ぶ。こうもりが自分の存在位置や障害物を知るために超音波を発して飛ぶことはよく知られているが、その性質上、ソナーや精密機器の洗浄などに利用されている。また空気中や水中では縦波だけが存在するが、固体中では縦波と横波（弾性波）が存在する。地震に「縦揺れ」「横揺れ」が存在することはご存知だろう。縦波と横波には、伝わり方に違いがあるので（特に、伝達する物質による速度差が大きい）、地震波は縦波が「初期微動」となる。

波動の基礎知識

波動について簡単な知識を持っておこう。波動とは（難しく定義すると）「ある物理量（位置、密度、電位など）が一箇所で振動的に変化（変位）して、その変化が次々に周囲に伝わっていく現象」である。水面に石を投げて波を発生させることがよく例として使われるが、この場合は変化している物理量は「位置」である。人間の耳に捉えられる空気中の音は、図のような密度の変化によって起こる。

 縦波と横波は、「物理量の変位が変位の進行方向（波の進行方向）と同じもの」と「変位が進行方向に対して垂直に起こるもの」の違いである。前者は、水平面に置いたバネで視認することができ、後者はゴムなどを弾いて見ることができる。上図から明らかなように、空気中を伝わる音は縦波である。楽器の振動は横波だが、その変位が空気に対して影響すると、空気の振動、すなわち縦波に変化する。この変化は物質の性質によるもので、地震波によって津波が起こるのもこの変化が起こるからである。

上記のような縦波ではなく、理解を易しくするために正弦波（水面の波動などを想像して欲しい）を例にとって、まず「波長」と「周期」を説明する。次図のような波形を考えたとき、山と山の間隔を波長、一つの山が過ぎてから次の山が来るまでの時間を周期と呼び、

 

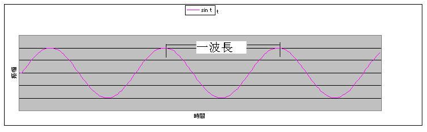
波の速さ＝波長／周期
の関係がある。周波数（振動数）は、通常一秒間の振動回数で表示される。442ヘルツとは、一秒間に442回の振動が起こることを意味する。前記のように、人間の可聴域（音として耳が認知できる振動数の範囲）は、個人差はあるが概ね20ヘルツから20000ヘルツである。

「正弦波」などという言葉を使うと、「わぁ、難しい！」というイメージを持たれるかもしれないが、できるだけ正確な言葉を使うことに慣れてほしい。上記の図は、ｙ＝sinｔというグラフで、高校時代に「三角関数」「円関数」などというテーマで見た記憶があるだろう。sin（正弦）、cos（余弦）などの「三角関数」として習ったものは、実は、波動そのものである。ここでは、縦方向は「大きさ」、横方向は「時間経過」を表している。

われわれが知っておくべき波の性質は、音程にまつわることが多い。うなり、差音などは波の性質から理解できるものであるし、音質も波の性質と密接な関係がある。波の性質を理解していると、奏法の理解にも役に立つ。知っておくべき基本は、複数の波相互の影響である。

 

二つの波が起こすこと

二つの波が重なり合うとき、波はお互いに影響し合う。簡単に言うと、二つの波の変位量を時間ごとに加えたものになる。

（注：グラフは、横方向が時間経過、縦方向が変位量になっている。二つの波を加えるとは、横方向の同じ位置にある二つのグラフの量を単純に加えただけである）

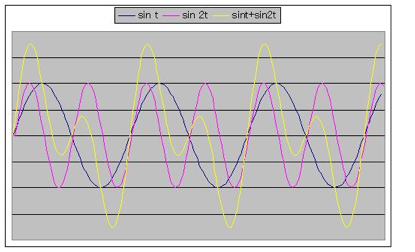
次図は、二つの波長の異なる正弦波を重ねたものである。

（参考図）二つの同じ正弦波を加えたもの：ｙ＝sinｔ＋sinｔ

 

◎　二つの異なる正弦波を加えたもの１：ｙ＝sinｔ＋sin２ｔ

 

◎　二つの異なる正弦波を加えたもの２：ｙ＝sin２ｔ＋sin３ｔ

 

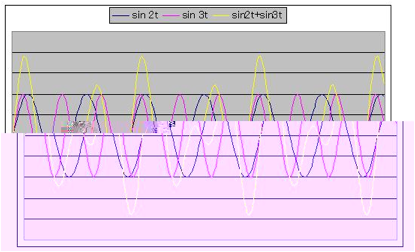
（注）これらの波は、始点（始まり）があって一つの方向に進むもの（進行波）であるが、実際の弦の振動はそうではない。弦の振動は、駒と指板の先端が固定されているもので、物理量の変移は一つの方向へ向かうのではなく、固定された二点間を往復する。このときに、「行き」の波と「反射した返り」の波が重なり合うと、進行しない波が現れる。こうした波動を「定常波」と呼ぶ。また、楽器の振動も、楽器という閉鎖空間での振動であり、進行波と定常波の一種が複雑に組み合わさったものである。これに対して、弦や楽器の振動が空気に伝わったときは、これまでの参考図のような進行方向を持った波となる。

うなり

　振動数のわずかに異なる二つの正弦波が同時に発生すると「うなり」が生じる。うなりは、「音」の問題ではなく、実は、波動の性質として説明されるものである。

＊＊＊＊＊＊＊＊＊　参考（ストリング誌の連載から）　＊＊＊＊＊＊＊＊＊

「うなり」を認知すること

前回述べたように、人間の耳は「簡単な整数比の周波数である二つの音」を「美しい＝はもる」と感知します。この「はもる」関係を、「純正な二音」と表現することにしましょう。同時に鳴る二つの音が簡単な整数比に近くなると、「わーん・わーん」という人間の耳が捉えることができる「うなり」を発するようになります。この「うなり」は、二音が簡単な整数比から少しばかり遠いと「わんわんわん」と細かく聞こえ、二つの音を純正に近づけていくと「わんわんわん」が「わーんわーんわーん」さらに「わーーーーんわーーーーん」と幅が広くなっていきます。最終的に二音が純正に非常に近くなると、このうなりは幅が広すぎて人間には認知できなくなります。「はもる」とは「うなりが聞こえない状態」であるとも言えます。

この「うなりが認知できない」音の間隔には若干の幅があります。今まで私が実験したところでは、ほぼ半数のレイトスターターがすぐにうなりを聴くことができましたが、最初は全くうなりを認知できない人も決して少なくありません。しかし、がっかりすることはありません。個人差や音の高さ、楽器の違いなどによって生じる差もありますので一概には言えませんが、前回述べたように「純正な二音を使って耳を鍛える」ことでほぼ純正に近いところまでうなりを聞きわけることができるようになるものです。

弦楽合奏の練習で、いろいろな組み合わせ（楽器の組み合わせ、位置の組み合わせ、音の高さの組み合わせなど）で実験をしてみると、「うなり」の聞きやすさにはかなり個人差があります。このうなりを聴く作業は純正な音程間隔を再現するための準備としてどうしても必要なことですから、なんとかして認識できるようにしたいものです。経験的には、最初はヴァイオリンよりヴィオラやチェロを聞く方が見つけやすいようです。

うなりの発生するしくみ

音は波です。振動数が多いほど高い音を、振動幅が大きいほど強い音になります。１秒間の振動数を「ヘルツ」と呼び、通常調弦に用いられるA音は440～443ヘルツの間です。このままでは細かすぎるので、１秒間に10回と11回の波を使ってうなりが発生する仕組みを説明します。

 

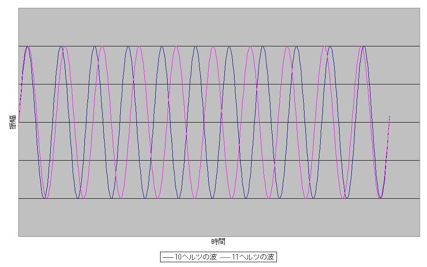
図表１は10ヘルツと11ヘルツの波が１秒間続いている図です。このように波がずれると、合成した別の波が発生します。この様子がわかるのが図表２です。

 

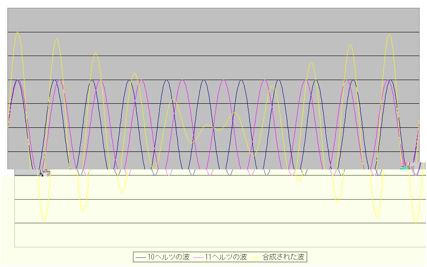
少し崩れたような波形が合成されたものですが、１秒間で１サイクルの動きになっていることがわかるはずです。これだけだとうなりに感じられませんが、図表３のように数秒間分グラフを描いてみると、うなりが発生している様子がわかります。

 

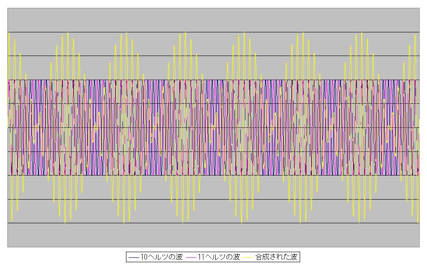
このように、うなりは周波数の「差」によってその周期が決まります。「１秒間に１回のうなり」が発生するということは、音の高低に関係なく、周波数差が１であることを示すことになります。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

（３）音とは何か

波の基礎知識を得たら、次は音について考えてみる。前述のように、音とは、非常に広い範囲の波動を示すが、通常は波動のうち、空気中の縦波でおよそ20Hzから20000Hzまでのものを呼ぶことが多い。ここでは、これを狭義の「音」と定義する。

この「音」は、これまで見てきた正弦波が基本である。この正弦波でできた単純な音を純音と呼ぶ。純音は実際の楽器から発せられることはなく、非常に近いものとしては、音叉の音や電気的な発信体（チューナーなど）から発せられる音がある。一般の音は単純な正弦波ではないが、振動数の異なる多くの正弦波が重ね合わさったものである（高校の数学で「フーリエ展開」を習った人もいるだろう）。これらのうち、比較的単純な正弦波が規則的に重なり合ったものを楽音と呼ぶ。我々が音として扱うもののほとんどは、この楽音である。さらに、振動が複雑であったり、規則的でないものを噪音と呼ぶ。ヴァイオリンで音程を表すことができるのは楽音で、「子音」は噪音である。

差音

これも波のいたずらである。周波数の異なる二つの波が同時に起こると、その周波数差の波が発生する。この、周波数の「差」で作られる音を、文字通り「差音」と呼ぶ。例えば、440HzのＡ音と330HzのＥ音が同時に鳴ったとき、その周波数の差である110HzのＡ音（440HzのＡ音の２オクターヴ下）も同時に鳴る。この関係は、周波数の比を使って簡単に求めることができる。上記の例なら、周波数比は３：４だから、発する差音の周波数比は１となる（単なる引き算）。

慣れるために、いくつかの差音を求めてみよう。
＊周波数比２：３の完全五度の場合、差音の周波数は（　　）となり、（　　　　　　　　）。
＊周波数比５：８の短五度の場合、差音の周波数は（　　）となり、（　　　　　　　　）。
＊周波数比３：５の長五度の場合、差音の周波数は（　　）となり、（　　　　　　　　）。

差音を聞くことができると、重音の音程を修正することやチューニングに効果がある。一方で、差音の影響で音程を勘違いしてしまうこともある。詳細は、音程講座の実戦編で述べる。

（４）音程を論じるために必要な数学的知識

「数学」などと言うとご大層だが、実際は小学生レヴェルの比の仕組みが理解できて使えればよい。敢えて触れる必要があるかどうかは疑問だが、これまでの説明で理解に時間がかかる人が少なくないので、簡単に触れておく。

「比」は、量をある基準を用いて、ある量をその基準と比較する手段である。200円の二倍は400円、と言った時、200円が基準で400円が比べられる量、二倍がその比に当たることはすぐにわかるはずだ。200円を１とすると、400円は２となる。基本的にはこれがわかっていればできるはず。音程理論では、まずシンプルに比を使ったものが出てくる。自然倍音列である。自然倍音列は、発する音の周波数を１としたときの、２倍音、３倍音・・・のことである。これらの音は、純正な音の関係を理解する前提となる。

次に、連比を復習しておこう。単純に言うと

「AとBの比が２：３、BとCの比が２：３の時に、A：Cの比を問う」

という問題が解ければよい。計算として解くならば、比の性質（比の前項と後項に同じ数をかけても比は変わらない）を利用して

A：B＝２：３＝４：６、B：C＝２：３＝６：９、とし、

A：B：C＝４：６：９　したがって、A：C＝４：９　を得る。

思い出していただけただろうか。これは、開放弦の周波数比にただちに結びつく。後述するように完全５度は２：３であるから、各開放弦の周波数比は

Ｇ：Ｄ＝Ｄ：Ａ＝Ａ：Ｅ＝２：３、となり、連比を取ると、

Ｇ：Ｄ：Ａ：Ｅ＝（　　）：（　　）：（　　）：（　　）となる。

ここまでがすんなりと理解できれば問題ないだろう。

５）音程を考える基礎となる協和する波動の比、計算練習を兼ねて

音程とは、二つ以上の音の間隔を言う。人間の耳は、周波数比が簡単な整数になる二つの音を協和すると感じる。

これは、少し考えれば簡単に理解できるだろう。第２項で述べたように、二つの波が同時に発生すると、お互いに影響し合って波形が変わるが、１：２や２：３などの周波数比を持つ二つの波動は、非常にシンプルな波形になる。鼓膜は空気の密度の差を振動として感知するが、波形が単純な方が能に伝わる電気信号もシンプルに、はっきりしたものになりそうなことは想像がつくはずだ。

それでは、実際の音程に当てはめて、周波数の関係を確認してみよう。

G線の１の指で押さえるA音の周波数を220とする。この周波数を二倍した440Hzの音は、１オクターヴ上のA音になる。元の音の周波数を１とすると、上の音は２になる。このように、周波数比が１：２の音は、オクターヴの関係になる。次に、完全五度の関係は２：３になる。440HzのA音（開放弦）の完全五度上のE（開放弦）を下のAと協和するように取ると、

A音：E音＝２：３、しかるにA音＝440Hz、ゆえに

　　２：３＝440：（　　　）となる。

逆に、開放弦のD音の周波数を求めてみよう。

D音：A音＝２：３、しかるに、A音＝440Hz、ゆえに

　　２：３＝（　　　）：440、となる。

（問）さらに、開放弦のG音の周波数を求めてみよ。

 

上記のように、周波数を実際の数値（ヘルツ）で用いるのは、非常に煩雑である。また、音程の理論を考えるためには周波数の絶対値が必要となることはなく、二つの音の周波数比がわかればよい。

（問）純正にあわせたヴィオラの四つの開放弦の周波数比を示せ。

 

次に、完全四度を考えてみよう。完全５度と完全四度がオクターヴを分割したものになることはお分かりだろう。すると、

C音：G音＝２：３、オクターヴすなわちC音：C（+1）音＝１：２（＝２：４）より、

C音：G音：C（+1）音＝２：３：４、となる。つまり、

完全四度、G音：C（+1）音＝３：４、であることがわかる。

天下り的だが、長三度の二音の周波数比は４：５になる。完全五度が２：３だから、長三和音（いわゆるドミソ）は、

C音：E音：G音　　　　　　C音：E音：G音　　　　　　C音：E音：G音

４ ： ５　　　　　　　　　　４ ： ５　　　　　　→　　 ４ ：５ ：６

２：　　： ３　　　→　　　４ ：　　： ６

となる。このことからただちに、短三度の周波数比が５：６であることがわかる。さらに、ここにC（+1）音とE（+1）を加えた比、

C音：E音：G音：C（+1）音：E（+1）音＝４：５：６：（　　）：（　　）

を利用すると、短六度、E音：C（+1）音＝５：（　　）、長六度、G音：E（+1）音＝６：（　　）＝３：（　　）がすぐにわかる。

（問）長三和音の構成音の周波数比は４：５：６だが、短三和音のそれはいかほどか。